Lens and Linear, 2048's logic in 22 lines

August 19, 2016

Last week a friend of mine asked me how I would implement the game 2048 in Java (at least the update logic) and we gave it a try. It went something like this:

So we need to represent the grid. I guess int[][] will do. Is this going to be an array of rows, or an array of columns? Either way we’ll need to stick to it. huh
Actually, it’ll be a sparse array, because not every cell will contain a value at all times. So an array of Maybe int. Oh right, Integer. We’ll need to remember to null-check. huh
The easiest would be to define the function to update a row/column once, and then apply it to the grid in different directions. Extract a row/column, process it, and place it back. Keeping track of the indices. huh

It is actually a problem that can be solved elegantly in Haskell using a few Isos and Traversals. We’ll use the linear library for representing the data and the lens library for accessing it.

You can find this code on Github and follow along in ghci.

Preparing the datatypes

We’ll represent our board as a 4 by 4 matrix from linear:

type Board = M44 (Maybe (Sum Integer))

This is a simple, row-major matrix from linear. In order to make our life simpler we’ll define a function to display the board:

λ: let display :: Board -> IO (); display = Boxes.printBox . mkBox

I made Board an instance of Default, so we can instantiate our first board as follows:

λ: let board = def :: Board

Let’s have a look:

λ: display board
X  X  X  X

X  X  X  X

X  X  X  X

X  X  X  X

Alright, nothing too exciting yet. This is simply a board filled with Nothings. We’ll use this to start discovering linear’s vector and matrix representation. A matrix of type M44 is nothing but a vector of vectors, stored in row-major order; a vector of matrix rows:

type M44 a = V4 (V4 a)  -- Defined in ‘Linear.Matrix’

The library has four very basic lenses for indexing into a vector: _x, _y, _z and _w. Let’s go to the second row (_y) of our board and set the fourth element (_w):

λ: import Control.Lens
λ: display $ board & _y . _w .~ (Just 2)
X  X  X  X

X  X  X  2

X  X  X  X

X  X  X  X

And it’s just that easy! Linear has a few other lenses for accessing elements and even vectors inside matrices. I definitely recommend checking it out.

22 Lines of logic

Let’s get back to our game. We first need an update function for the rows/columns. The game 2048 actually does not care about empty cells, wherever they are, it’ll just ignore them:

2 X 2 X             X X X 4
-------     --->    -------
X X 2 2             X X X 4

In this small example the user swiped right, and even though the rows differed, the result was the same (it’s not injective). We’ll simply take a list containing the non-empty cells as an input, and output a list of the resulting non-empty cells. Here are a few examples:

[2, 2]    -> [4]
[1, 2, 2] -> [1, 4]
[2, 1, 2] -> [2, 1, 2]
[2, 2, 2] -> [4, 2]

We’ll specify some rules that might not correspond exactly to what the original game uses, but that will be good enough for us. When traversing a list:

If two neighbors are equal, replace them by their sum.

The above is easily translated to Haskell code:

merge :: (Eq a, Monoid a) => [a] -> [a]
merge (x:x':xs) | x == x' = (x <> x') : merge xs
merge (x:xs)              = x : merge xs
merge []                  = []

Note
We’ve used a slightly more abstract version than [Int] -> [Int]. This is useful for several reasons. For instance you might not have decided yet what type you are going to use to represent your cells (Int? Integer? An enumeration of the powers of two?). Also you might want to add a UI. In this case you will want to remember which cells were merged together so that you can play an animation. Below we will be using Sum Integer, the integers with addition as the monoidal composition (<>).

There’s not much room for error. GHC infers that we have covered all input cases, and we only need to make sure that the code reflects the rule above. We can open up ghci and verify with our (limited) test-suite:

λ: merge [2, 2] :: [Sum Integer]
[4]

λ: merge [1, 2, 2] :: [Sum Integer]
[1, 4]

λ: merge [2, 1, 2] :: [Sum Integer]
[2, 1, 2]

λ: merge [2, 2, 2] :: [Sum Integer]
[4, 2]

Now we need to apply merge to different parts of the board. This is where the lens library comes in handy. More importantly linear’s good support for various types of lenses, particularly Isos and Traversals. Here’s my (intuitive) understanding of those:

If you need to go back and forth between two datatypes a and b, you’ll need an Iso' a b.
If you need to get several bs from a datatype a, you’ll need a Traversal' a b.

Earlier we prepared a Board. Now we have a function that operates on [a]. We’ll want to traverse our board to get lists. We’ll want a Traversal' Board [a]. Or rather several Traversal' Board [a], one for each of the four orientations:

rows, wors, cols, locs :: Traversal' (M44 (Maybe  a)) [a]

The various directions are represented here:

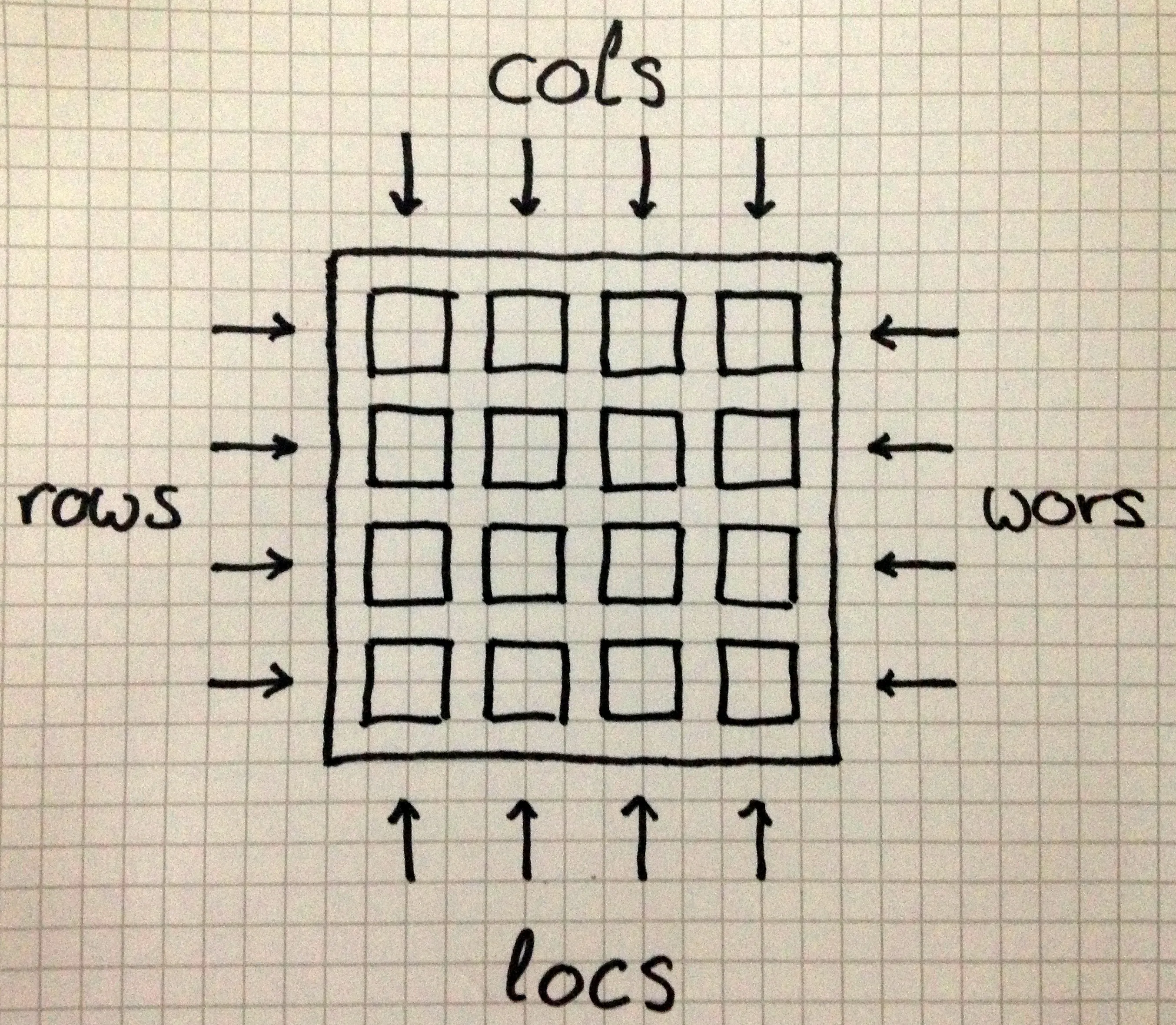
Setting up our lenses

Let’s start with rows. Once again, the type M44 is nothing but a vector of vectors, or a V4 of V4s.

The vector type V4 is an instance of Traversable (not Traversal, which is a type) so we can use traverse:

λ: :t traverse
traverse :: (Applicative f, Traversable t) => (a -> f b) -> t a -> f (t b)

Simply put, traverse says

If your t is Traversable, I’ll give you Traversal' (t a) a for free.

Since M44 a is V4 (V4 a)) it says:

Your V4 is Traversable, so I’ll give you Traversal' (M44 (Maybe a)) (V4 (Maybe a)).

Good, so now we know how to get/set/act on each row of our board independently. Problem is that when traversing it, we are given the rows as V4 (Maybe a)s. But our function merge works on [a]s! Here come the Isos. We need an Iso that allows us to go back and forth between V4 (Maybe a) and [a]. The lens library comes with a handy function iso which builds an Iso from a pair of inverse functions. Here’s what we’ll use:

list :: Iso' (V4 (Maybe a)) [a]
list = iso toList fromList
  where
    toList v = reverse $ catMaybes $ foldl (flip (:)) [] v
    fromList (xs :: [a]) = V4 (xs^?ix 0) (xs^?ix 1) (xs^?ix 2) (xs^?ix 3)

We have two operations here: toList and fromList. The first one simply copies all the Just values of a V4 into a list, that is

toList :: V4 (Maybe a) -> [a]

whereas, on the other hand, fromList recreates a vector from a list. Since there can be fewer than four values in a list, fromList adds as many Justs as possible to the V4, and fill the rest with Nothings. You will notice that this also takes care of “shifting” the values to the beginning of the vector.

And, believe it or not, we’re almost done implementing our rows function. Here’s the last bit:

rows = traverse . list

We traverse our matrix one row at a time, but before handing the row to the caller, we transform it to a list using toList. And when we’re handed back a list, we insert it in the matrix as a row using fromList. Let’s see the result by setting all rows to [1,2,3]:

λ: display $ board & rows .~ [1,2,3]
1  2  3  X

1  2  3  X

1  2  3  X

1  2  3  X

For a few Isos more

Now, let’s get started on wors, which should give us the reversed rows (when reading a row we start from the right-most element). The lens library has another handy abstraction: Reversing. Any type that is an instance of Reversing gets the reversed iso for free. Let’s make V4 an instance of Reversing:

instance Reversing (V4 a) where
  reversing v = V4 (v^._w) (v^._z) (v^._y) (v^._x)

and wors can now be implemented:

wors = traverse . reversed . list

Facile, non? We get (vector) rows through traverse, reverse them, and then turn them into a list.

λ: display $ board & wors .~ [1,2,3]
X  3  2  1

X  3  2  1

X  3  2  1

X  3  2  1

On to the next one: cols. Getting columns is easy: transpose the matrix. The columns of the original matrix are now the rows of the transposed matrix. Earlier we used the iso function to build an Iso' between V4 (Maybe a) and [a]. We’ll use it again to create an Iso between a matrix and its transposed self:

transposed :: Iso' (M44 a) (M44 a)
transposed = iso transpose transpose

(If you know of a function f = join iso, please ping me. I couldn’t find it.)

And now the two implementations for the columns and reversed columns:

cols = transposed . rows
locs = transposed . wors

λ: display $ board & cols .~ [1,2,3]
1  1  1  1

2  2  2  2

3  3  3  3

X  X  X  X

λ: display $ board & locs .~ [1,2,3]
X  X  X  X

3  3  3  3

2  2  2  2

1  1  1  1

Extra lens goodness

And that’s it, we’ve implemented the logic of the game! Believe it or not, it didn’t take us more than 22 lines of code. But make no mistake. Lenses aren’t for code golfing. They’re just well-crafted, type-safe abstractions. A lot of code was already written on top of those, meaning there’s a lot of stuff you can reuse. Also, when used properly, they should allow you to write less of your own code. I believe that (other things being equal) it is always better: less room for mistakes, less code to maintain, less code newcomers have to understand.

As opposed to the simplistic Java given in the introduction:

We don’t care (too much) if a matrix is a vector of rows or a vector or columns (row-major or column-major). The Linear library abstracts this for us and gives us a few functions to use in order to traverse the matrix.
No null checks.
Thanks to lens, we haven’t used a single index explicitly. All the getting, updating and setting of values was declarative. Each indexing of an element has its own function: if an element is not there, the function is not there.

Finally, we can wire everything together, making use this time of lens’ support for actions in the state monad:

data Action = Up | Down | Left | Right

play :: (MonadState Board m) => Action -> m ()
play Up    = cols %= merge
play Down  = locs %= merge
play Left  = rows %= merge
play Right = wors %= merge

Let me know if you enjoyed this article! You can also subscribe to receive updates.

Here's more on the topic of Haskell:

Puzzle solving in Haskell